La teoria dell’informazione di Claude Shannon

Nell’ultimo articolo pubblicato, per distinguere l’informazione in generale dall’informazione giornalistica facevo l’esempio del “chiedere un’informazione”. Se ne potrebbero fare molti altri.

Ne prendo in prestito un esempio, molto particolare, dalla voce “Cibernetica” del Dizionario di filosofia di Abbagnano:

Se, avendo visto un oggetto in una certa direzione (cioè avendone ricevuto un messaggio visivo), stendo il braccio per afferrarlo e sbaglio la direzione o la distanza, subito l’informazione di questo sbaglio rettifica il movimento del mio braccio e mi consente di dirigerlo esattamente verso l’oggetto: sia l’operazione, sia la correzione dell’operazione stesso sono in questo caso guidati da messaggi cioè da informazioni ricevute o trasmesse dal sistema nervoso che dirige il movimento del braccio.
[Dizionario di filosofia, III edizione, Cibernetica, p. 154]

Anche solo questi due esempi (quello sopra citato e il “chiedere un’informazione”), penso diano l’idea di quanto sono variegati gli usi che facciamo di questa parola.

Solo in parte questo modo più generale di intendere l’informazione ha a che fare con l’informazione giornalistica a cui forse siamo più abituati a pensare.

Per occuparci un po’ più da vicino del significato generale dell’informazione possiamo sfruttare alcuni concetti della cosiddetta teoria dell’informazione, una proposta elaborata a partire da metà Novecento che ha avuto grande importanza nella comprensione e nell’elaborazione di questa nozione.

Il saggio che ha fatto iniziare questi studi è A Mathematical Theory of Communication di Claude E. Shannon. In tale saggio Shannon analizzava la comunicazione avvalendosi delle proprie competenze matematiche.

La teoria dell’informazione ha contribuito sensibilmente allo sviluppo di numerose tecnologie, e l’articolo sopra citato è divenuto rapidamente un “classico”. Esso ha infatti introdotto un gran numero di concetti e di formule fondamentali per la ricerca successiva.

Si tratta di un articolo importante ma estremamente ostico per i non matematici e i non addetti ai lavori. Non essendo neanche lontanamente in grado di dare una ricostruzione delle teorie contenute nell’articolo di Shannon, né tantomeno del dibattito successivo, ho pensato di ricostruire alcuni punti cardine della teoria dell’informazione basandomi sulla sintesi che di essa fa il Dizionario di filosofia di Abbagnano alla voce Cibernetica (le citazioni le prendo da lì):

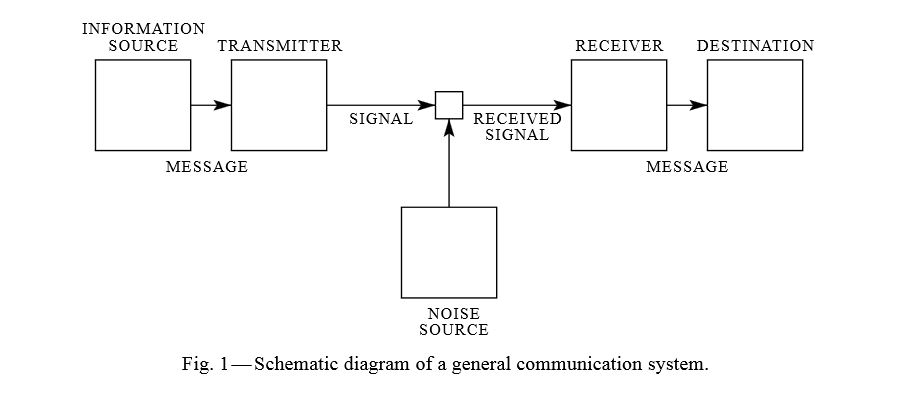
1. L’informazione sembra avere uno schema composto da almeno tre elementi: il messaggio emesso, la trasmissione e il messaggio ricevuto.
   In realtà però le cose sono quasi sempre più complesse. Il messaggio emesso è infatti la messa in codice di ciò che l’emittente vuole trasmettere. Tale messaggio messo in codice viene poi decodificato dal ricevente.
   Tale processo è ben esemplificato dal telegrafo. Un messaggio viene codificato e poi decodificato. In realtà però questo schema può essere applicato in tutti i casi in cui c’è passaggio di informazioni. Ad esempio anche una “frase pronunciata in italiano deve essere compresa secondo le regole e il dizionario della lingua italiana e non apporterà alcuna informazione a chi non conosce l’italiano”.
   Essendo le informazioni inserite all’interno di un processo, sono possibili “errori di trasmissione”, in varie fasi, durante il passaggio di informazioni.



2. A Mathematical Theory of Communication di Shannon parte proprio da questa possibilità di equivoci e di interferenze durante la trasmissione di un messaggio.
   Ricordo un gioco che facevamo da bambini, “il telefono senza fili”. Ci si metteva seduti uno accanto all’altro e si decideva chi doveva incominciare il gioco. Il bambino che iniziava inventava una frase e la sussurrava nell’orecchio dell’amico vicino che a sua volta la ripeteva all’orecchio del bambino seduto accanto, e così via…In più si era a giocare, più era improbabile che la frase ascoltata dall’ultimo bambino fosse identica a quella inventata all’inizio.
   Imparavamo, giocando, come i messaggi siano difficili da trasmettere se i “passaggi” sono tanti.
   Torniamo alla teoria dell’informazione. Shannon osserva che il messaggio inviato attraverso un qualsiasi tipo di canale subisce delle deformazioni e perciò una parte delle informazioni vanno perdute durante la trasmissione. Il matematico statunitense mise in analogia tale perdita d’informazione con l’entropia, la nota funzione che esprime la degradazione dell’energia che si verifica in ogni trasformazione del lavoro meccanico in calore.
3. Basandosi su tale analogia tra l’entropia e il passaggio di informazioni Shannon approccia al calcolo della quantità di informazione intesa come entropia negativa. La quantità d’informazione/entropia negativa decresce continuamente mentre l’entropia positiva (la perdita d’informazione), aumenta.
   Shannon quindi applica, con vari accorgimenti, il calcolo delle probabilità della termodinamica all’informazione. L’informazione entra quindi nell’affascinante campo della probabilità.
4. Non avventurandosi più di tanto nella ricostruzione teorica dell’articolo di Shannon, il Dizionario di filosofia sintetizza: “In generale si può dire che più un messaggio è improbabile, maggiore è l’informazione che esso trasmette”. Sarebbe interessante capire più nel dettaglio come la teoria dell’informazione sia arrivata a questa affermazione, anzi se siete esperti in materia, spiegatecelo nei commenti.
   In generale però, è un’affermazione che si può capire facendo dei semplici esempi. Un evento certo, ad esempio il fatto che domani sorgerà il sole, non sorprende nessuno. Non ha quindi alcun valore informativo. E’ vero invece l’opposto, un evento altamente improbabile ha un alto valore informativo.
5. La quantità minima d’informazione si ha quindi quando c’è una scelta solo tra due possibilità equiprobabili. Shannon chiama l’unità minima d’informazione bit (binary information unit).

Questa ricostruzione, molto approssimativa e parziale, può comunque essere utile, credo. Una cosa che mi ha colpito, lo scrivevo sopra, è di come tale teoria sia nota come Teoria dell’informazione, eppure Shannon nel titolo del suo importante articolo scrive “communication” e non “information”.

Quest’altra parola, “comunicazione”, riguarda anch’essa questo blog se non altro perché è la parola in cui si è soliti racchiudere il settore in cui lavoriamo. Comunicazione e informazione sono sinonimi? Sono parole intercambiabili?

Penso di no. Nel prossimo post elencherò alcune differenze tra informazione e comunicazione, secondo me rilevanti…